In 1874 Georg Cantor opened a can of mathematical worms by proving the real numbers comprise a larger infinity than do the integer numbers. It turns out that mathematical infinity comes in different sizes. To understand this, we need to review the different kinds of numbers.
The Natural and Integer Numbers
Numbers begin with the recognition that some things group together — sheep and apples, for example. One can have a flock of sheep or a bushel of apples. Sheep and apples (and many other things) are similar enough to each other to be considered members of a group based on those similarities.
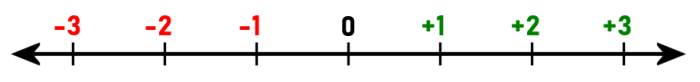
Given a group of objects, an obvious property is how many items are in the group — the size of the group. This is the foundation of counting. These “counting” numbers are called the natural numbers (and represented by the Blackboard bold symbol ℕ).
They start at zero1 and continue 1, 2, 3, 4, 5, … to infinity.2
The natural numbers let us put useful labels on how many sheep or apples we have. They also allow us to compare flocks and bushels to see if one is bigger than the other. Better yet, they let us do some arithmetic. We can add or multiply any two natural numbers and get a natural number result.3
Subtraction is a problem, though. We get a natural number with 8-5=3, but if we turn it around, 5-8=?, we don’t.4 If we create negative versions of the natural numbers, though, then we’re okay: 5-8=-3. Same qualitative answer but negative, which gives numbers a directionality.
This new set of numbers, the (positive) natural numbers plus the negative natural numbers, give us the integer numbers (represented by the symbol ℤ5). These are also called the whole numbers.
And now subtraction works.
The Rational Numbers
Sometimes arithmetic demands a part (or fraction) of an integer. For instance, it’s easy to evenly divide 12 into two parts (6 in each) or three parts (4 in each), but what if we want to divide it into five parts? The integers don’t allow an answer.
Enter the rational numbers (denoted ℚ6). These are numbers in the form a/b where a and b are integers. Now we can divide 12 into five parts, each containing 12/5.
Rational numbers can be as small or as large as desired, so for a long time the Ancient Greeks thought these were all math and geometry required. In this newsletter’s last post, Proof of the Irrational, I wrote about how they found out they were wrong.
Bottom line, though: we need yet another new kind of number.
The Real Numbers
Beyond the integer numbers, beyond the rational numbers, arithmetic forces us to accept another new kind of number, the real numbers (denoted ℝ). These include the irrational numbers, which cannot be represented by integer or rational numbers.

Unlike the natural, integer, or rational numbers, which have steps between them, the real numbers present a smooth continuum of numbers. They are metaphorically “analog” to the “digital” of the other three.
The real numbers solve many issues in math and physics but also turn out to be problematic for math and physics.7 A quote by Leopold Kronecker (1823–1891), “God made the integers, all else is the work of man” speaks to this.
Enumerating Different Types of Numbers
The natural numbers go from zero to “infinity” — the word we use to mean “goes on forever”. Infinity is not a number; it’s an abstract idea. We can’t know how many natural numbers there are, but we have a process for listing all of them: start at zero and keep adding one:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, …
We can list (enumerate) the integer numbers by starting at zero and generating two new numbers each time by both adding and subtracting one:
0, -1, +1, -2, +2, -3, +3, -4, +4, -5, +5, …
We can even list the rational numbers, although it’s ever so slightly trickier. We just need to recognize that numbers in the form a/b (with a and b integers) form a 2D grid:
Which we can enumerate starting from the upper left corner and then tracing the diagonals from the leftmost column up to the topmost row:
We manually add a zero (0/1) to start the sequence.8
Note the semi-colon-separated sub-sequences (each is a diagonal). The sum of numerator and denominator remains constant within a given upwards diagonal. The sum increases by one in each new sub-sequence (as does the length). Generating the ever-increasing sub-sequences is the actual protocol.
Counting the Natural, Integer, and Rational Numbers
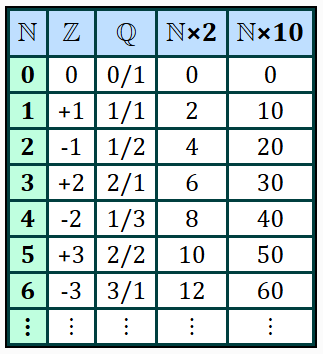
Crucially, in all three cases so far, we have an enumeration protocol that, given any number, tells us what the next number is. The natural, integer, and rational numbers are all countable. Because of this, we can create a list relating the natural counting numbers to the integer and rational numbers:
I added two other enumerable sequences, the even natural numbers and the natural numbers multiplied by ten. The point is that, although each is infinite, they map to each other. We can establish a one-to-one relationship between them. For example, the last and first columns are related by one being ten times the other.
This means that each of these number types, despite being infinite, are the same “size” of infinity. We call this size of infinity aleph-zero (and denote it with the symbol ℵ₀). It has the distinction of being a “countable” (or enumerable) infinity as the table above illustrates.
Two crucial points: Firstly, in the abstract, given infinite time, it’s possible to list all members of a countable infinity because of the enumeration protocol. Secondly, note that an infinite subset of the natural numbers (such as the even numbers) still has the same size of infinity. Weirdly, with infinity, subsets of it have the same size.
But…
The real numbers present a problem. What’s the next number after zero? Another way to put it: what’s the first non-zero positive real number? There isn’t one. There is no such thing as the smallest positive real number.9
In fact, given any real number, it’s not possible to name the next real number. Each real number is an isolated island with no other land in sight.10 What’s the next number after pi? Or before it? There isn’t one!
To put it formally, there is no successor function for the real numbers, so there is no obvious way to enumerate them. Like the integer and rational numbers, they are infinite in both the positive and negative directions, but is the infinity of non-enumerable things the same as the infinity of enumerable things?
Spoiler: No. The real numbers are significantly different from the natural, integer, and rational numbers. They comprise a larger infinity.
The Diagonal Trick
Now we’re ready to explore Cantor’s diagonal trick.
Imagine there is a magical function that, given a natural number, returns a unique real number. We can make an infinite list of real numbers using the magic function and the row number to get the real number for the row:
1: f(1) = 0.458668437217145779477486438785...
2: f(2) = 0.233248578549467614967616741786...
3: f(3) = 0.882319276262899363585711362756...
4: f(4) = 0.121483681269887685355383347122...
5: f(5) = 0.129247723893857158384499191295...
6: f(6) = 0.321478855945973952938946642347...
7: f(7) = 0.989915916384311822582535414746...
...A few things about this list: Firstly, we only care about real numbers greater than 0.0 and less than 1.0. They are enough to make the point. Secondly, each entry has an infinite string of decimal digits. That’s not actually possible, but in this idealized thought experiment, these are considered real numbers with infinite decimal expansions.11 Lastly, we ignore f(0)=0.000… because we only care about numbers greater than zero here.
Note that this list is infinite in two dimensions. Each entry is infinite, and the list itself is infinite. (This is, in fact, the problem.)
But we assume a magic function that returns every real number given every natural number. So, it seems we have found a way to enumerate the real numbers. The list appears random to us, but the magic function ensures a unique number for each row number. The list is infinite, so we do give the magic function every natural number (except zero).
Therefore, we assume the list has every real number between 0.0 and 1.0.
But Cantor demonstrated a contradiction:
The highlighted diagonal picks out single digits from each row (and each column). Since the list is 2D-infinite, the diagonal is infinite.
Below the list, I’ve copied the diagonal digits. Below them is a new(!) number created by adding +1 to each digit of the diagonal number. This new number is different from every number on the list because its:
First digit is different from the first number.
Second digit is different from the second number.
Third digit is different from the third number.
…and so on to infinity…
This new number cannot be on the list!
Note we can create many new numbers. The second new(!!) number above comes from adding +2 rather than +1. The third new(!!!) number above comes from adding +9. We can add any single digit (other than zero, which does nothing).12
We can also use patterns of digits (for instance +1, +2, +3, +1, +2, +3, … or +2, -2, +2, -2, … or whatever we can conceive).
And we’re not limited to the basic diagonal:
Any diagonal works so long as it takes one digit from each row and column. Here, again, the possibilities are endless.
We can make infinitely many numbers that cannot be on the list.
What Does This Mean?
We assumed the list was complete but found it cannot be. This contradiction means our assumption is false. There is no magic function. The real numbers are not enumerable. It is not possible, even in principle, to generate a complete list of them. We can try the diagonal trick to add new numbers to the list, but the diagonal logic applies all over again. The list can never be complete.
More importantly, this shows that the real numbers comprise a larger infinity than the natural, integer, or rational numbers. A key question in mathematics is whether the size of the real numbers is indeed the next size of infinity - whether it is ℵ₁ (aleph-one).
As an aside, Cantor’s diagonal trick underlies both Gödel’s Incompleteness theorems and Turing’s Halting Problem theorem. Both are examples of systems (math theorems and computer programs) that cannot be enumerated.
That we have two infinities, ℵ₀ and ℵ₁, suggests more, and indeed Cantor devised a hierarchy of ever-increasing infinities based on power sets. As someone with constructivist leanings, I’m a bit askance at these higher infinities. I think the more realistic view is that there is ℵ₀ and ℵ₁ — countable and uncountable — and the latter seem decidedly non-physical and abstract to me.
Perhaps Kronecker was right after all, at least in terms of physical reality.
Until next time…
Some people think they start at one. But they’re wrong.
To “infinity”, but not beyond.
It turns out that this ability to do arithmetic is what ends up demanding ever more interesting (and capable) kinds of numbers.
If you want eight apples but I only have five, you’ll have to adjust your expectations.
For “Zahlen”, which is “numbers” in German.
For “quotient”.
E.G. If an electron is a negatively charged point with no size, then it’s possible to get infinitely close to it. But charge is inversely related to distance, so as distance decreases to zero, charge increases to infinity. But electrons obviously can’t have infinite charge.
There’s a minor annoyance involved with zero. Note how values can be repeated, for instance 1/1, 2/2, 3/3, and so forth are all equal to one. (The yellow numbers in the table.) The table protocol as described doesn’t create distinct values, but distinct fractions.
We can add a leftmost column for 0/n (but not a topmost row for n/0 because division by zero is undefined). Then the upper-left corner will be 0/1, and we get the zero for free. But we also then get another series of repeated values: 0/2, 0/3, 0/4, etc. These are valid fractions (all equal to zero), so having a zero column might be preferable.
Even if we could imagine one, there can always be a smaller one.
There is likewise no smallest positive rational number, nor is there a successor function for the numerically “next” rational number, but the integer nature of a/b allows an enumeration protocol, so there is a function for their enumeration.
You can make a specific jump, say to the island plus one your value or twice your value. But it’s a blind jump “by name” to another isolated island.
Even 1.0 is technically 1.000… as a real number.
If adding a given value makes the result a double-digit, use only the last digit. So, 9+1=10=0 and 8+3=11=1.







I really hope this post was inspired by my joke about escaping reality by means of.... well, heavily abused set theory lol. Very well done.