Group Theory Notes & Homework
A page of notes and homework for the Introduction to Group Theory posts on Words Without Knowledge by David. This is a work in progress.
Lessons
Lesson IX
Lesson VIII
Lesson VII
Theorem: Let G and G' be groups, and ϕ : G → G’ be a homomorphism. Then the left and right cosets of ker(ϕ) are the same – that is, ker(ϕ) is normal. Furthermore, a and b are in the same coset of ker(ϕ) if and only if ϕ(a) = ϕ(b).
I’m just not grokking the proof in the first section. I follow that a ker(ϕ) = b ker(ϕ) is the aH operation of left cosets, so ah and bh for h ∈ ker(ϕ). I follow the algebra all the way to the left side of:
But I don’t see how the right side follows. And I wallow from that point on.
I’m doubly confused by “…which means that ab⁻¹ ∈ ker(ϕ). Thus, ab⁻¹ ∈ ker(ϕ), which means they are in the same right coset as well.” The phrasing makes me think the second expression should differ from the first. And I don’t follow the conclusion. Why are they also in the right coset?
I’ve done multiple examples of all the expressions, but still can’t seem to get the lightbulb to turn on. Frustrating!
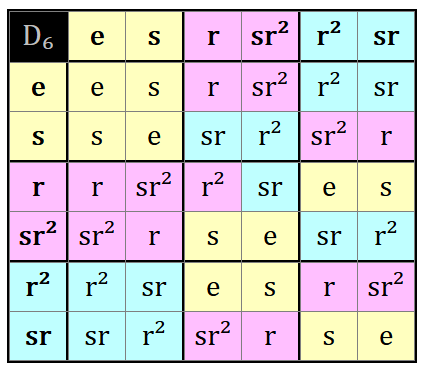
Cosets as colors: Note that the cosets of H = {e,s} in D₆ show H is not normal, so we cannot construct the same table we did with the cosets of H = {e, r, r², r³} in D₈:
Definition: Let H be a subgroup of G. If, for all cosets aH and bH of H, and all a₁, a₂ ∈ aH, b₁, b₂ ∈ bH, we have a₁b₁, a₁b₂, a₂b₁, a₂b₂ ∈ cH, then (aH)(bH) = cH, and G induces its operation on the left cosets of H. And so, (aH)(bH) = (ab)H.
Using the cosets of 5ℤ in ℤ, with H={.., -5, 0, +5,..}:
a₁, a₂ ∈ a₁H, a₂ = a₁h | h ∈ H
b₁, b₂ ∈ b₁H, b₂ = b₁j | j ∈ H
2H: 2+5ℤ = {.., -8, -3, 2, 7, 12,..} | a₁=-3, a₂=7 | 7 = -3+h | h=10 ∈ H
3H: 3+5ℤ = {.., -7, -2, 3, 8, 13,..} | b₁=-2, b₂=8 | 8 = -2+j | j=10 ∈ H
a₁b₁ ∈ (a₁b₁)H, a₂b₂ ∈ (a₁b₁)H ⇒ a₂b₂ = a₁b₁k | k ∈ H
-3 + -2 = -5 ∈ (-3 + -2)H = (-5)H = H
7 + 8 = 15 ∈ (-3 + -2)H = (15)H = H ⇒ 7 + 8 = -3 + -2 + k | k=20 ∈ H
a₁b₂ = a₁(b₁j) = (a₁b₁)j ∈ H
a₂b₁ = a₂(b₂j⁻¹) = (a₂b₂)j⁻¹ = (a₁b₁)kj⁻¹ ∈ (a₁b₁)H
-3 + 8 = -3 + (-2 + 10) = (-3 + -2) + 10 = 5 ∈ H
7 + -2 = 7 + (8 + -10) = ( 7 + 8) + -10 = (-3 + -2) + 20 + -10 = 5 ∈ HGeneralizing:
a₂ + b₂ = (a₁ + 5r) + (b₁ + 5s) = a₁ + b₁ + 5(r + s) ∈ (a₁ + b₁) + 5ℤ.
a₂ + b₂ = (a₁ + h₁) + (b₁ + h₂) = a₁ + b₁ + (h₁ + h₂) ∈ (a₁ + b₁) + H.Bottom line, we need (a₁ + b₁) and (a₂ + b₂) in the same coset.
Using a homomorphism from ℤ₆ to ℤ₃:
ϕ: ℤ₆ → ℤ₃ = {(x mod 3) | x ∈ ℤ₆}
G = {0, 1, 2, 3, 4, 5}
G' = {0, 1, 2}
H = ker(φ) = φ⁻¹[{0}] = {x ∈ ℤ₆ | φ(x) = 0} = {0, 3}
Cosets of H:
0H = {0, 3} = H0 = H
1H = {1, 4} = H1
2H = {2, 5} = H2
3H = {3, 0} = H3 = H
4H = {4, 1} = H4 = 1H = H1
5H = {5, 2} = H5 = 2H = H2
Three cosets: {0,3}, {1,4}, {2,5}
H is normal: xH = Hx
a ker(ϕ) = b ker(ϕ) = a+{0,3} = b+{0,3} = {a,a+3} = {b,b+3}
{2, 5} = {5, 2} | a=2, b=5 | a & b are in same coset
{2, 5} ≠ {4, 1} | a=2, b=4 | a & b NOT in same coset1. Go back to the proof that the kernel of a homomorphism is normal and show that assuming a and b are in the same right coset of ker(ϕ) implies that they are in the same left coset.
Attempting to ape the proof from the text:
Assume ker(ϕ) a = ker(ϕ) b. Then b = ha | h ∈ ker(ϕ).
Multiplying by a⁻¹ on the right gives: ba⁻¹ = h | h ∈ ker(ϕ).
So: ϕ(ba⁻¹) = ϕ(b)ϕ(a⁻¹) = ϕ(b)ϕ(a)⁻¹ = e'.
And: ϕ(b⁻¹a) = ϕ(b⁻¹)ϕ(a) = ϕ(a⁻¹)ϕ(a) = e'??
...
I may just have to take the L on this one. 😟2. Find a homomorphism ϕ : ℤ₆ → ℤ₃ with kernel H = {0, 3}.
ϕ: ℤ₆ → ℤ₃ = {(x mod 3) | x ∈ ℤ₆}
ker(φ) = φ⁻¹[{0}] = {x ∈ ℤ₆ | φ(x) = 0} = {0, 3}3 Find an isomorphism ϕ : ℤ/nℤ → ℤₙ, where ℤ/nℤ is the set of cosets of nℤ in ℤ.
ϕ: ℤ/nℤ → ℤₙ = {H=0, 1+H=1, 2+H=2, ..., (n-1)+H=(n-1)} | H = nℤ}4. Let G₁ and G₂ be groups. Define the cartesian product G₁ × G₂ to be the set of pairs (g₁, g₂), where g₁ ∈ G₁ and g₂ ∈ G₂. Then we can define a group operation on G₁ × G₂ by (g₁,g₂)⋅(h₁,h₂) = (g₁⋅h₁, g₂⋅h₂).
That is, we're doing the group operation "coordinate−wise". Show that G₁ × G₂ is indeed a group under this operation. (An example of this cartesian product would be ℤ₂ × ℤ₂: it would have elements (0, 0), (0, 1), (1, 0), and (1, 1).)
G₁ × G₂ is a group because it has an identity element, (0,0), is closed under the operation, and every element has an inverse (x,y)⁻¹ = (M-x, N-y), where M and N are the number of rows and columns, respectively.
Examples, assuming ℤ₄×ℤ₄:
(0,0)⋅(1,1) = (0⋅1, 0⋅1) = (1,1)
(1,1)⋅(3,3) = (1⋅3, 1⋅3) = (0,0)
(1,1)⋅(1,1)⁻¹ = (1,1)⋅(4-1, 4-1) = (1,1)⋅(3,3) = (0,0)
This works because the row and column labels are themselves an additive group, ℤₙ, and the operation acts on row and column labels separately, which preserves the two groups.5. Let G₁, G₂ be groups. Let π₁: G₁ × G₂ → G₁ be defined by π₁(a, b) = a, and let π₂: G₁ × G₂ be defined by π₂(a, b) = b. Show that π₁, π₂ are homomorphisms. (These are called the canonical projection maps, because we're "projecting" our larger group G₁ × G₂ onto G₁ or G₂.)
The functions π₁ and π₂ partition G₁×G₂ into the cosets of their respective kernels. There will be M row cosets and N column cosets, where M and N are the number of rows and columns respectively:
Cosets of ker(π₁) are:
0H = H0 = {(0,0), (0,1), (0,2), ... (0,N-1)}
1H = H1 = {(1,0), (1,1), (1,2), ... (1,N-1)}
2H = H2 = {(2,0), (2,1), (2,2), ... (2,N-1)}
: :
(M-1)H = H(M-1) = {(M-1,0), (M-1,1), (M-1,2), ... (M-1,N-1)}
Cosets of ker(π₂) are similar but with row/column swap.
These are both homomorphisms because:
π₁((g₁,g₂) • (h₁,h₂)) = π₁((g₁•h₁), (g₂•h₂)) = (g₁•h₁) =
π₁(g₁,g₂) • π₁(h₁,h₂) = (g₁)•(h₁) = (g₁•h₁)
π₂((g₁,g₂) • (h₁,h₂)) = π₂((g₁•h₁), (g₂•h₂)) = (g₂•h₂) =
π₂(g₁,g₂) • π₂(h₁,h₂) = (g₂)•(h₂) = (g₂•h₂)6. What is the kernel of π₁, and what is the kernel of π₂?
ker(π₁) := φ⁻¹[{0}] = {(0,0), (0,1), (0,2), ... (0,N-1)}
ker(π₂) := φ⁻¹[{0}] = {(0,0), (1,0), (2,0), ... (M-1,0)}Lesson VI
Equivalence relation: a ~ b. The relation here is a⁻¹b ∈ H, with H ⊆ G and a,b ∈ G. The cell of a group partition with element a (where a ∈ G) is all x ∈ G where a⁻¹x ∈ H, or a⁻¹x=h, where h ∈ H. Multiplying both sides by a we have x=ah.
Left coset: aH := {ah | h ∈ H}. Right coset: Ha := {ha | h ∈ H}
Normal: aH = Ha | a ∈ GTheorem: Let H be a subgroup of G. Then for any a ∈ G, the coset aH has the same size as H.
Theorem: (Lagrange's Theorem) Let H be a subgroup of a finite group G. Then the order of H is a divisor of the order of G.
Definition: Let G be a group and a ∈ G. Then the set {aⁿ | n ∈ ℤ} is called the cyclic subgroup of G generated by a. We denote this group by ⟨a⟩ and say that a is a generator of ⟨a⟩.
Theorem: Every group of prime order is cyclic.
Definition: Let H be a subgroup of G. The number of cosets of H in G is called the index of H in G, which we denote (G : H).
Definition: Let H be a subgroup of G. We say that H is a normal subgroup of G if for all g ∈ G, gH = Hg. We denote this by H ⊴ G.
Exercise 1: Compute the cosets of 5ℤ = {..., -10, -5, 0, 5, 10, ...} in ℤ. Make sure you understand why the left and right cosets have to be the same!
0+H = {..., -10, -5, 0, +5, +10, ...} = H+0 = H
1+H = {..., -9, -4, +1, +6, +11, ...} = H+1
2+H = {..., -8, -3, +2, +7, +12, ...} = H+2
3+H = {..., -7, -2, +3, +8, +13, ...} = H+3
4+H = {..., -6, -1, +4, +9, +14, ...} = H+4
The left and right cosets match because integer addition is communitive.Exercise 2. Find a subgroup of D₈ that does not have the same left cosets as right cosets; that is, find a subgroup of D₈ that is not normal.
G = D₈, H={e, s}
[ eH = sH = {e, s} ] = [ He = Hs = {e, s} ] = H
[ rH = sr³H = {r, sr³} ] ≠ [ Hr = Hsr = {r, sr} ]
[ r²H = sr²H = {r², sr²} ] = [ Hr² = Hsr² = {r², sr²} ]
[ r³H = srH = {r³, sr} ] ≠ [ Hr³ = Hsr³ = {r³, sr³} ]
rH ≠ Hr and r³H ≠ Hr³ so H={e, s} is not normal.A question:
H: e ⋅ s = s; s ⋅ e = s.
rH: r ⋅ sr³ = sr²; sr³ ⋅ r = s.
r²H: r² ⋅ sr² = s; sr² ⋅ r² = s.
r³H: r³ ⋅ sr = sr²; sr ⋅ r3 = s.
Hr: r ⋅ sr = s; sr ⋅ r = sr².
Hr²: r² ⋅ sr² = s; sr² ⋅ r² = s.
Hr³: r³ ⋅ sr³ = s; sr³ ⋅ r³ = sr².
So, (a⁻¹b = h | a,b ∈ G, h ∈ H) is not true for all elements in a coset?Exercise 3. Let G be a group with order 48. What are the possible orders of subgroups of G?
2 (24 members each), 3 (16 members each), 4 (12 members each), 6 (8 members each), 8 (6 members each), 12 (4 members each), 16 (3 members each), 24 (2 members each).Exercise 2 involves a subgroup of D₈ that is not normal. The D₈ subgroup H = {e, r, r², r³} is, though, and it can be used to form a table similar to the one in the post:
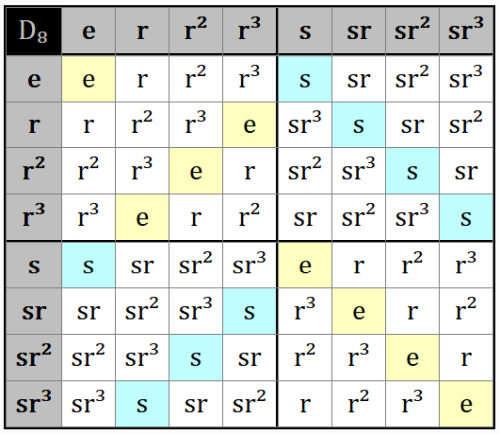
Note that the upper left and lower right quadrants contain only members from H, and the lower left and upper right quadrants contain only members from its complement, G-H.
Lesson V
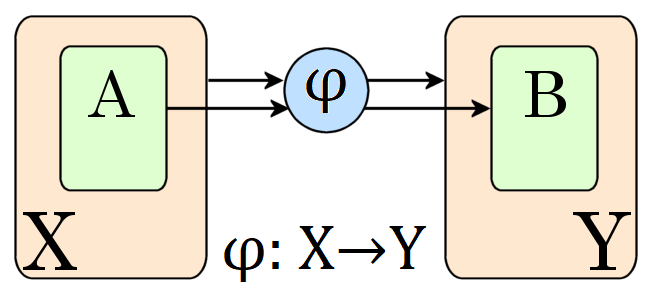
Image and preimage, given φ : X → Y and A ⊆ X and B ⊆ Y:
φ[A] := {φ(a) | a ∈ A} (image of A under φ)
φ⁻¹[B] := {a ∈ A | φ(a) ∈ B} (preimage of B under φ)Theorem: Let φ : G → G’ be a homomorphism.
If e ∈ G is the identity element, then φ(e) is the identity element e' ∈ G'.
If a ∈ G, then φ(a)^{-1} = φ(a^{-1}).
If H is a subgroup of G, then φ[H] is a subgroup of G'.
If K' is a subgroup of G', then φ^{-1}[K'] is a subgroup of G.
Kernel, given φ: G → G’:
Kernal: ker(φ) := φ⁻¹[{e'}] = {x ∈ G | φ(x) = e'}A kernel is the preimage of {e’} where e’ ∈ G’ and e’ is 𝕀 in G’.
Theorem: Let G and G' be groups, and φ : G → G' be a homomorphism. Then φ is injective if and only if φ has trivial kernel - that is, ker(φ) = {e}.
Exercise 1: In the proof of our first theorem, we left it to the reader to show that K contains the identity and inverses. Show that K indeed contains the identity and inverses.
Since K' is a group, it contains the identity, e', and inverses. Therefore, we have φ(e)=e' and K contains the identity. If a' ∈ K' is an inverse, then we have φ(a)=a', so K contains the inverses.Exercise 2: Using the homomorphism you found last week from D₈ into S₄, compute the images of the sets A = {e, s} and B = {e, r, r^2, r^3}.
φ[A] = φ[{e, s}] = {φ(e), φ(s)} = {e', (12)(34)}
φ[B] = φ[{e,r,r²,r³}] = {φ(e),φ(r),φ(r²),φ(r³)} = {e',(1234),(13)(24),(1432)}Exercise 3: Construct a homomorphism from S₃ to S₄ with non-trivial kernel.
φ: S₃→S₄ := [e=e,(123)=e,(132)=e, (23)=(12)(34),(12)=(12)(34),(13)=(12)(34)]
Essentially, looking at S₃ as D₆, all proper rotations go to S₄ [1234] and all improper rotations go to S₄ [2143] (an improper rotation of D₈).
For ker(φ) we have φ(e)=e', φ(r)=e', φ(r²)=e'
So: φ⁻¹[{e'}] = {a ∈ S₃ | φ(a) = e'} = {e, r, r²}That last one was a toughie!
Lesson IV
Given two groups G and H:
Homomorphism: φ(a•b) = φ(a)•φ(b) | a,b ∈ G | φ(x) ∈ HNote the left operation is in G but the right operation is in H.
Isomorphism: S₃ ≅ D₆ (a homomorphism & bijection)For example: Starting with ℤ₁₂, φ: ℤ₆→H, φ(x) = 2x is an isomorphism.
Exercise 1: We know that S₃ and D₆ are isomorphic, but the isomorphism we found is from S₃ to D₆. Can you find an isomorphism that's from D₆ to S₃? (Keep in mind that we know an "inverse" function has to exist, since the isomorphism we found is a bijection.)
φ: D₆ → S₃ := [e→e, r→(123), r²→(132), s→(23), s⋅r→(12), s⋅r²→(13)]Exercise 2: Find a homomorphism from D₈ into S₄.
φ: D₈ → S₄ :=
[e→e, r→(1234), r²→(13)⋅(24), r³→(4321), s→(12)⋅(34), s⋅r→(13), s⋅r²→(14)⋅(23), s⋅r³→(24)]Exercise 3: Find a homomorphism from S₃ into S₄.
φ: S₃ → S₄ "S₄ subset [?,?,?,4]; 6 elements" :=
[e→e, (12)→(12), (13)→(13), (23)→(23), (123)→(123), (132)→(132)]It’s getting harder! The first one was pretty obvious, but the other two were tougher.
Lesson III
Subgroups. H⊆G means H is a subgroup of G. The improper subgroup is G⊆G, all others are proper. The subgroup {e} is the trivial subgroup, all others are nontrivial. Write H ≤ G to mean H is possibly improper and H < G if H is proper.
A subgroup is a group, so has the same properties as groups (identity, closed, inverses, associative).
A cyclic group has a generator such that every member can be written as gⁿ for some g ∈ G and n ∈ ℤ. For example, ℤ₁₂ has generators 1, 5, 7, and 11 (remember that the operation in ℤ₁₂ is addition).
Exercise 1: We saw that there is a subgroup of size 6 for the group ℤ₁₂. What other sizes of subgroup exist? (Don't forget the trivial subgroup and the improper subgroup.)
Subgroups of order 2, 3, and 4 also exist (plus 1 and 12). (see below)Exercise 2: When we first tried to construct a subgroup of ℤ₁₂, we started with
H = {0, 1}. The issue we ran into was that 1 generated all of ℤ₁₂. What other numbers generate ℤ₁₂? Do you see anything interesting about those numbers in relation to the number 12?
1: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
2: [0, 2, 4, 6, 8, 10]
3: [0, 3, 6, 9]
4: [0, 4, 8]
5: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
6: [0, 6]
7: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
8: [0, 4, 8]
9: [0, 3, 6, 9]
10: [0, 2, 4, 6, 8, 10]
11: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11]
The numbers 5, 7, and 11 also generate ℤ₁₂. They are not factors of 12. All factors of 12 (other than 1 and 12) result in proper subgroups.This was fun!
Lesson II
Permutations of elements (such as S₃ = {1, 2, 3}) can also form a group.
Z₁₂ (a clock) is a group {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
The identity element is always unique. An element’s inverse is always unique.
Functions. f: G → H. Domain (G) and codomain (H).
Injective: Into. Every f(g)=h, for g ∈ G, has a unique h, for h ∈ H. Formally:
Injective: a=b ⇔ f(a)=f(b) | a,b ∈ G | f(a),f(b) ∈ HSurjective: On top of (covering). Every h, for h ∈ H, has at least one f(g), for g ∈ G.
Bijective: One-to-one. Both injective and surjective.
Given bijection f: G → H, then f⁻¹: H → GExercise 1: Choose any permutation in S₃ — that is, any permutation of three elements — and show that it is an injection and a surjection (and, therefore, a bijection).
S₃ = {1, 2, 3}Exercise 2: Think about the groups D₆ and S₃. Do you see any relation between them? Each group has 6 elements — see if you can find some kind of natural "correspondence" between the two.
D₆ = {e, r, r², s, sr, sr²}, S₃ = {e, (123), (132), (23), (12), (13)}
Rotations in D₆ match cycles in S₃, and swaps D₆ match those in S₃.
e ≅ e
r ≅ (123)
r² ≅ (132)
s ≅ (23)
sr ≅ (12)
sr² ≅ (13)Exercise 3: (Challenging) How many elements are in S₄? What about S₅, and in general Sₙ?
S₄ has 24 elements (see below for a full listing).
S₅ has 120 elements.
Sₙ has n! elements (as permutations like this do).Lesson I
Rotations and swaps of regular polygons can form a group.
group ≡ (G, •) "G has members or elements"
• is a closed binary operation "addition, multiplication, other".
The operation is associative but may not commute (be Abelian).
G must have an identity, often written as e.
For every a ∈ G, there is a unique b ∈ G (aka a⁻¹) such that a•b=b•a=e.Introduction of triangle symmetries, D₆ (aka D₃, depending on your religion).
Exercise 1: For each element of D₆, find an inverse for that element. (Don't worry about the uniqueness of the inverse - we'll show that in full generality next time.)
D₆ = {e, r, r², s, sr, sr²}
e ⋅ e = e
r ⋅ r² = e
r² ⋅ r = e
s ⋅ s = e
sr ⋅ sr = e
sr² ⋅ sr² = eExercise 2. Show that the symmetries of a square, which is called D₈, is a group. You can assume that composition is associative.
D₈ = {e, r, r², r³, s, s⋅r, s⋅r², s⋅r³}
D₈ has an identity element, e, and inverses for all elements, and the operation is closed, so D₈ is a group.Set Definitions
Regular Polynomials
D₆ "triangle" = {e, r, r², s, s⋅r, s⋅r²}

Some useful identities:
rs = sr² , rsr = s , rsr² = sr
r²s = sr , r²sr = sr², r²sr² = s
ss = e , srs = r² , sr²s = rD₆ cosets for H = {e, r, r²}:
eH = {e , r , r² } = H = He = {e, r, r²}
rH = {r , r², e } = H = Hr = {r, r², e}
r²H = {r², e , r } = H = Hr² = {r², e, r}
sH = {s , sr, sr²} = sH = Hs = {s , rs , r²s } = {s, sr², sr}
srH = {sr, sr², s } = sH = Hsr = {sr , rsr , r²sr } = {sr, s, sr²}
sr²H = {sr², s, sr } = sH = Hsr² = {sr², rsr², r²sr²} = {sr², sr, s}
Two cosets: H and sH.
H is normal: xH = Hx.D₆ cosets for H = {e, s}:
Left cosets of H:
eH = {e , s} = H
rH = {r , rs} = {r, sr²}
r²H = {r², r²s} = {r², sr}
sH = {s , e} = H
srH = {sr, srs} = {sr , r²} = r²H
sr²H = {sr², sr²s} = {sr², r} = rH
Right cosets of H:
He = {e , s} = H
Hr = {r , sr} = {r, sr²}
Hr² = {r², sr²} = {r², sr}
Hs = {s , e} = H
Hsr = {sr, ssr} = {sr , r} = Hr
Hsr² = {sr², ssr²} = {sr², r²} = Hr²
Three left cosets: H, rH, and r²H.
Three right cosets: H, Hr, and Hr².
H is NOT normal: rH ≠ Hr and r²H ≠ Hr²φ: D₆ → S₃ := [e→e, r→(123), r²→(132), s→(23), s⋅r→(12), s⋅r²→(13)]
Cosets for H = ker(φ) = {e}:
eH = {e} = He
rH = {r} = Hr
r²H = {r²} = Hr²
sH = {s} = Hs
srH = {sr} = Hsr
sr²H = {sr²} = Hsr²
Six cosets of H: the elements of D₆
H is normal: xH = Hxφ: D₆ → ℤ₂ := [0 if g = rⁿ else 1] = {0, 0, 0, 1, 1, 1}
Cosets for H = ker(φ) = {e, r, r²} (because φ({e, r, r²})=0):
eH = {e, r, r²} = H = He = {e, r, r²}
rH = {r, r², e} = H = Hr = {r, r², e}
r²H = {r², e, r} = H = Hr² = {r², e, r}
sH = {s, sr, sr²} = sH = Hs = {s , rs , r²s } = {s , sr², sr }
srH = {sr, sr², s} = sH = Hsr = {sr , rsr , r²sr } = {sr , s , sr²}
sr²H = {sr², s, sr} = sH = Hsr² = {sr², rsr², r²sr²} = {sr², sr , s }
Two cosets of H: H and sH
H is normal: xH = HxD₈ "square" = {e, r, r², r³, s, s⋅r, s⋅r², s⋅r³}
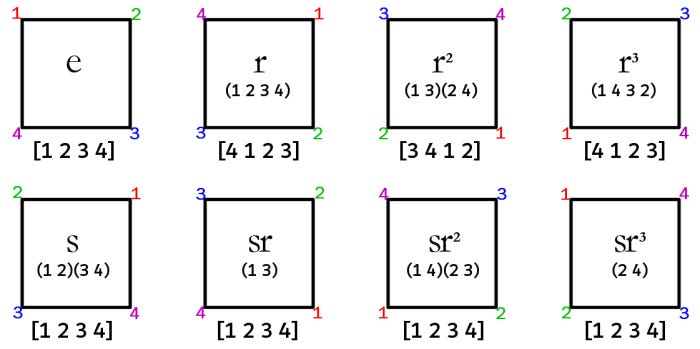
Some useful identities:
es = s
rs = sr³ , rsr = s , rsr² = sr , rsr³ = sr²
r²s = sr² , r²sr = sr³ , r²sr² = s , r²sr³ = sr
r³s = sr , r³sr = sr² , r³sr² = sr³ , r³sr³ = s
ss = e , srs = r³ , sr²s = r² , sr³s = rD₈ cosets for H = {e, r, r², r³}:
Left cosets of H:
eH = {e , r , r² , r³ } = H
rH = {r , r² , r³ , e } = H
r²H = {r² , r³ , e , r } = H
r³H = {r³ , e , r , r² } = H
sH = {s , sr , sr², sr³} = sH = G-H
srH = {sr , sr², sr³, s } = sH
sr²H = {sr², sr³, s , sr } = sH
sr³H = {sr³, s , sr , sr²} = sH
Right cosets of H:
He = {e , r , r² , r³ } = H
Hr = {r , r² , r³ , e } = H
Hr² = {r² , r³ , e , r } = H
Hr³ = {r³ , e , r , r² } = H
Hs = {s , sr³, sr², sr } = Hs = G-H
Hsr = {sr , s , sr³, sr²} = Hs
Hsr² = {sr², sr , s , sr³} = Hs
Hsr³ = {sr³, sr², sr , s } = Hs
Two cosets: H and sH
H is normal: xH = HxD₈ cosets for H = {e, s}:
Left cosets of H:
eH = {e , s } = H = He
rH = {r , sr³ } = sr³H ≠ Hr
r²H = {r² , sr² } = sr²H = Hr²
r³H = {r³ , sr } = srH ≠ Hr³
sH = {s , e } = H = Hs
srH = {sr , r³ } = r³H ≠ Hsr
sr²H = {sr², r² } = r²H = Hsr²
sr³H = {sr³, r } = rH ≠ Hsr³
Right cosets of H:
He = {e , s } = H
Hr = {r , sr } = Hsr
Hr² = {r² , sr²} = Hsr²
Hr³ = {r³ , sr³} = Hsr³
Hs = {s , e } = H
Hsr = {sr , r } = Hr
Hsr² = {sr², r² } = Hr²
Hsr³ = {sr³, r³ } = Hr³
Four left cosets: H, rH, r²H, r³H.
Four right cosets: H, Hr, Hr², Hr³.
H is NOT normal: rH ≠ Hr and r³H ≠ Hr³Sequences
S₃ “ABC” = {
1: [1, 2, 3]: e,
2: [1, 3, 2]: (23),
3: [2, 1, 3]: (12),
4: [2, 3, 1]: (132)
5: [3, 1, 2]: (123),
6: [3, 2, 1]: (13),
}S₄ “ABCD” = {
1: [1, 2, 3, 4]: e,
2: [1, 2, 4, 3]: (34),
3: [1, 3, 2, 4]: (23),
4: [1, 3, 4, 2]: (243),
5: [1, 4, 2, 3]: (234),
6: [1, 4, 3, 2]: (24),
7: [2, 1, 3, 4]: (12),
8: [2, 1, 4, 3]: (12)⋅(34),
9: [2, 3, 1, 4]: (132),
10: [2, 3, 4, 1]: (1432),
11: [2, 4, 1, 3]: (1342),
12: [2, 4, 3, 1]: (142),
13: [3, 1, 2, 4]: (123),
14: [3, 1, 4, 2]: (1243),
15: [3, 2, 1, 4]: (13),
16: [3, 2, 4, 1]: (143),
17: [3, 4, 1, 2]: (13)⋅(24),
18: [3, 4, 2, 1]: (1423),
19: [4, 1, 2, 3]: (1234),
20: [4, 1, 3, 2]: (124),
21: [4, 2, 1, 3]: (134),
22: [4, 2, 3, 1]: (14),
23: [4, 3, 1, 2]: (1324),
24: [4, 3, 2, 1]: (14)⋅(23)
}(an ongoing page)